OPEN-SOURCE SCRIPT
Gaussian Average Convergence Divergence
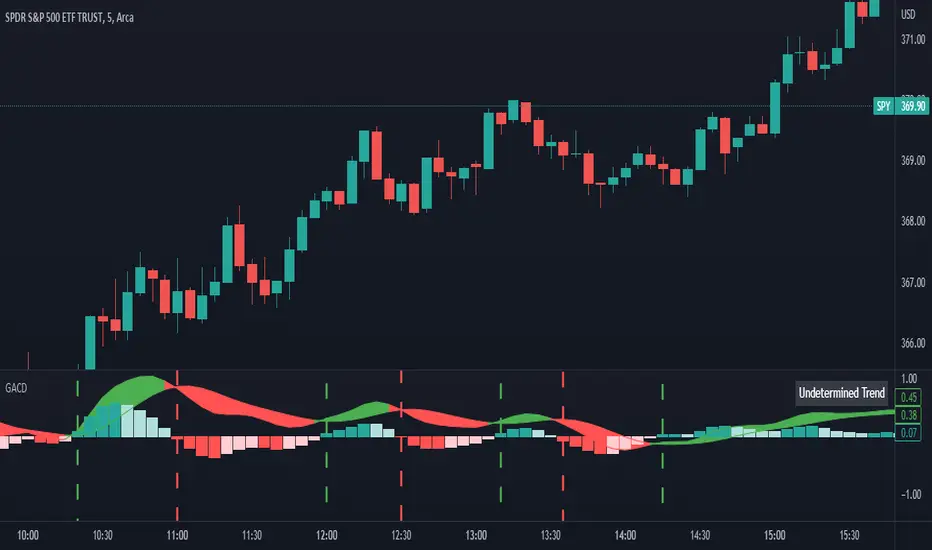
What exactly is the Ehlers Gaussian filter?
This filter is useful for smoothing. It rejects higher frequencies (fast movements) more effectively than an EMA and has less lag. John F. Ehlers published it in "Rocket Science For Traders." Dr. René Koch was the first to implement it in Wealth-Lab.
The transfer response of a Gaussian filter is described by the well-known Gaussian bell-shaped curve. Only the upper half of the curve describes the filter in the case of low-pass filters. The use of gaussian filters is a step toward achieving the dual goals of lowering lag and lowering the lag of high-frequency components relative to lower-frequency components.
From Ehlers Book: "The first objective of using smoothers is to eliminate or reduce the undesired high-frequency components in the price data. Therefore these smoothers are called low-pass filters, and they all work by some form of averaging. Butterworth low-pass filters can do this job, but nothing comes for free. A higher degree of filtering is necessarily accompanied by a larger amount of lag. We have come to see that is a fact of life."
References John F. Ehlers: "Rocket Science For Traders, Digital Signal Processing Applications", Chapter 15: "Infinite Impulse Response Filters"
This filter is useful for smoothing. It rejects higher frequencies (fast movements) more effectively than an EMA and has less lag. John F. Ehlers published it in "Rocket Science For Traders." Dr. René Koch was the first to implement it in Wealth-Lab.
The transfer response of a Gaussian filter is described by the well-known Gaussian bell-shaped curve. Only the upper half of the curve describes the filter in the case of low-pass filters. The use of gaussian filters is a step toward achieving the dual goals of lowering lag and lowering the lag of high-frequency components relative to lower-frequency components.
From Ehlers Book: "The first objective of using smoothers is to eliminate or reduce the undesired high-frequency components in the price data. Therefore these smoothers are called low-pass filters, and they all work by some form of averaging. Butterworth low-pass filters can do this job, but nothing comes for free. A higher degree of filtering is necessarily accompanied by a larger amount of lag. We have come to see that is a fact of life."
References John F. Ehlers: "Rocket Science For Traders, Digital Signal Processing Applications", Chapter 15: "Infinite Impulse Response Filters"
Notas de prensa
- Made some changes that optimized the code- Added different customization options
- Chart Updated
Notas de prensa
- Fixed bug with colors- Added custom band settings
Notas de prensa
- Updated more customization options for vertical lineNotas de prensa
- Updated bug with band fillScript de código abierto
Siguiendo fielmente el espíritu de TradingView, el autor de este script lo ha publicado en código abierto, permitiendo que otros traders puedan entenderlo y verificarlo. ¡Olé por el autor! Puede utilizarlo de forma gratuita, pero tenga en cuenta que la reutilización de este código en la publicación se rige por las Normas internas. Puede añadir este script a sus favoritos y usarlo en un gráfico.
Exención de responsabilidad
La información y las publicaciones que ofrecemos, no implican ni constituyen un asesoramiento financiero, ni de inversión, trading o cualquier otro tipo de consejo o recomendación emitida o respaldada por TradingView. Puede obtener información adicional en las Condiciones de uso.